pca
pca-主成分分析
b站链接：https://www.bilibili.com/video/BV1E5411E71z?from=search&seid=12219938521484233618
PCA主要用于数据降维与表面法向量估计等。
数据降维的目的用更少的空间保留尽可能多的信息。主成分就是所有数据投影到这个方向时，能够保留最大的信息（即方差最大）。假想下图中的二维点如果投影到某个方向时变成了一个点，那么就没有保留到原始的分布信息，所以要求方差最大，就是想把差异最大化，从而保留原始数据的分布特点。
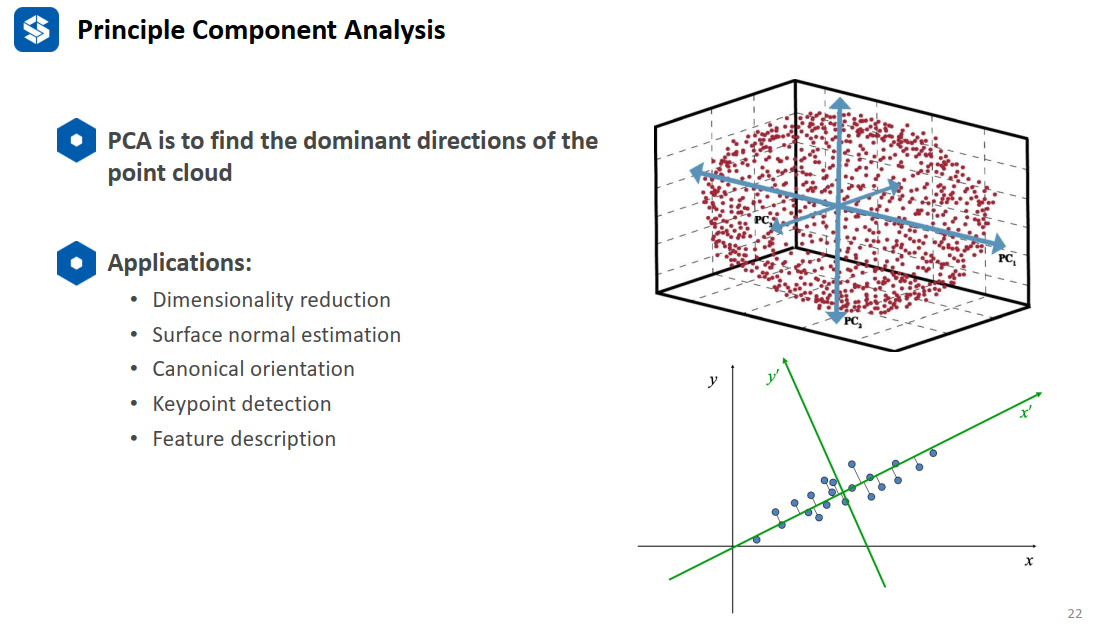
求解主成分
协方差矩阵的推到，过程不用记：
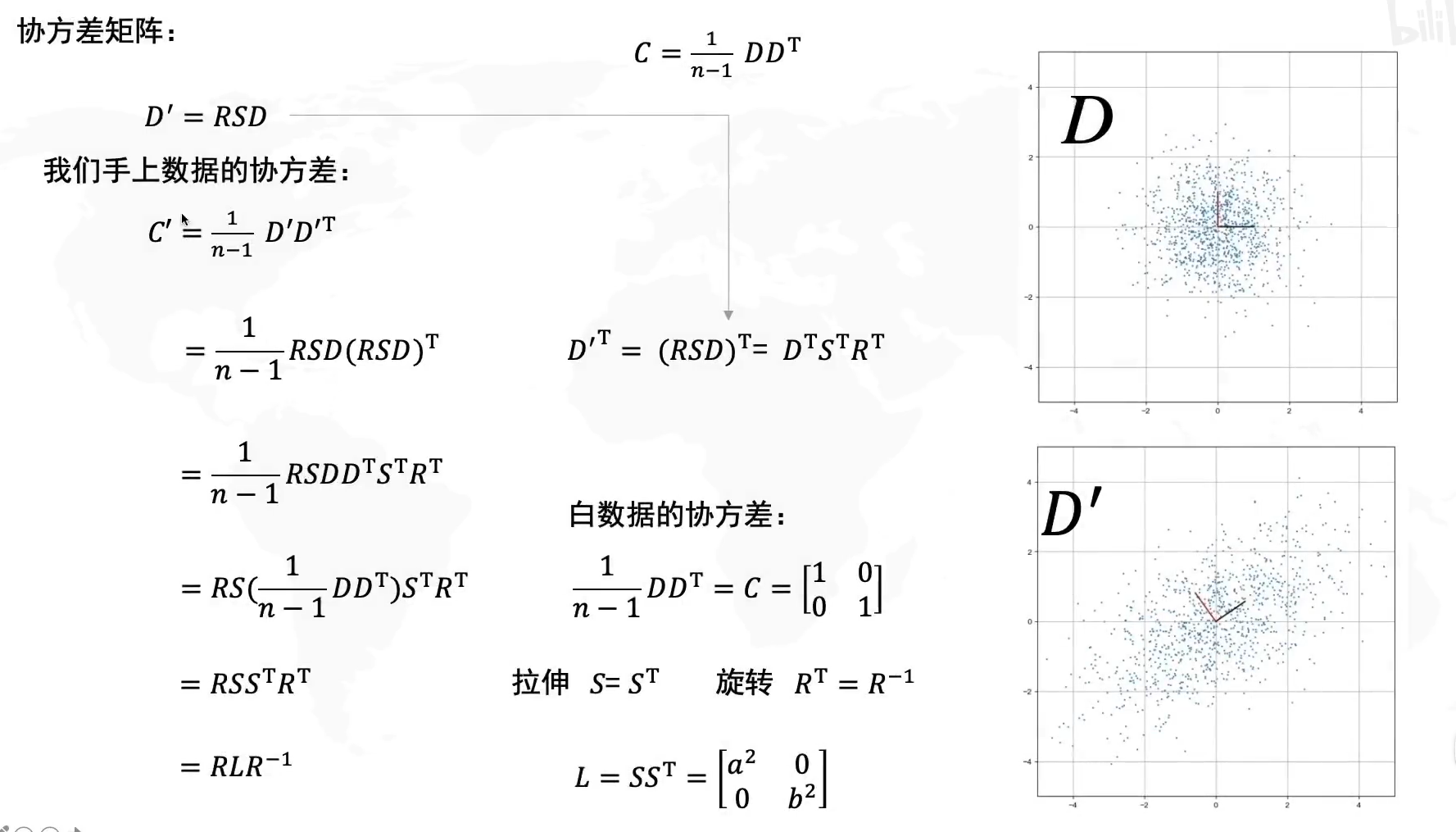主成分为旋转矩阵R的列向量。
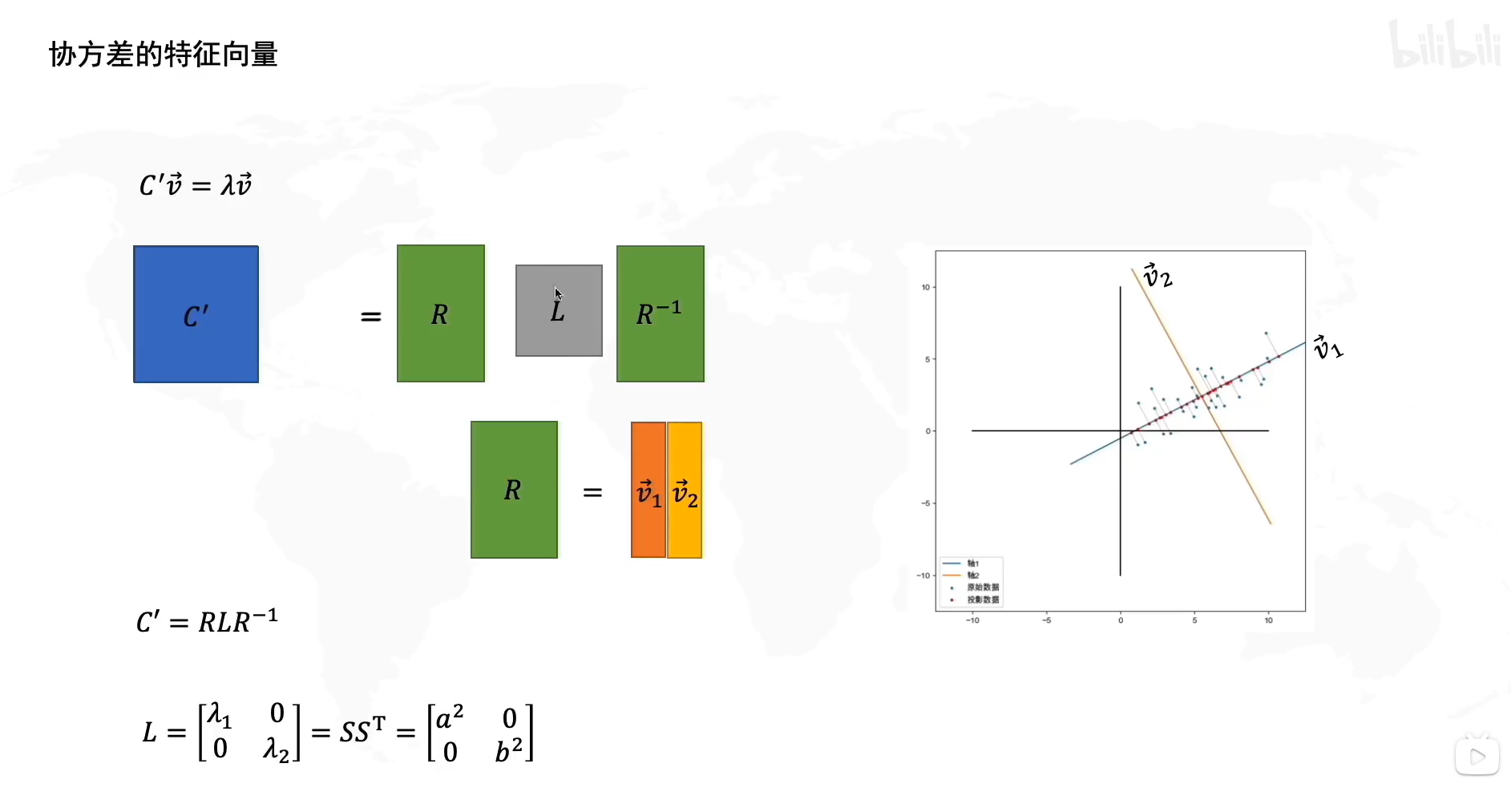
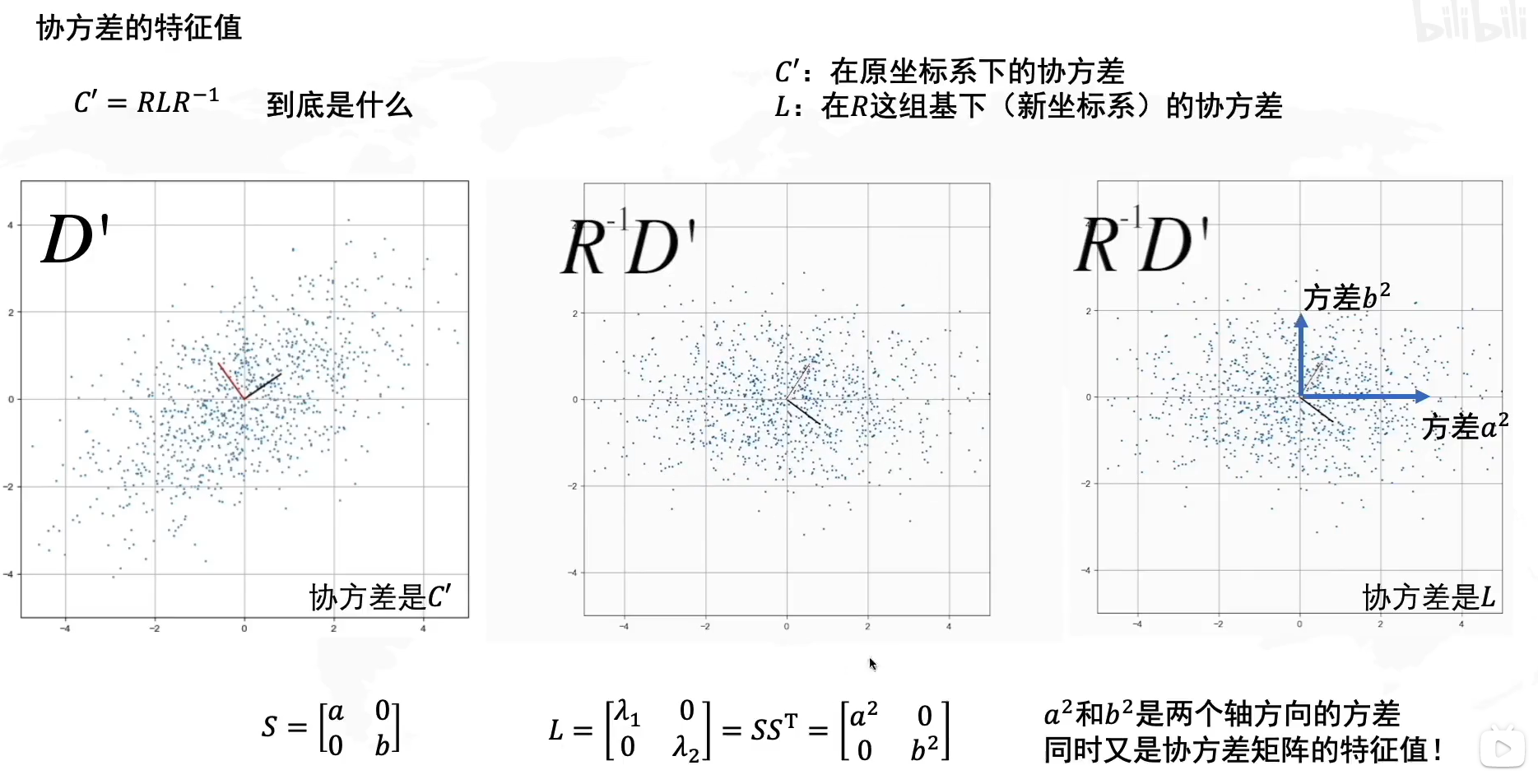
协方差的特征值：
评论区
这是挖掘数据线性分布规律的最重要算法。其实不仅仅用来降维，凡是涉及到分析数据分布特点的都可以用到。如：现在获得了某曲面大量的采样点云，要估计曲面在某采样点的法向量方向。则通过PCA分析该点及周围采样点的分布规律，找到数据点分布离散程度最大的两个正交方向，则这两个方向就近似构成曲面在该点的切平面，与此两方向正交的第三个方向就是曲面在该点的近似法矢
最初知道这个算法就是在研究点云处理、逆向工程时查文献了解的。后来开始转向机器学习又遇到这个。后面学了矩阵论加强了线代基础，把这个算法自己又推导了一遍，在看此视频之前已经从理论到直观透彻理解了