RANSAC

RANSAC——随机一致性采样

RANSAC 主要解决样本中的外点问题，最多可处理 50% 的外点情况。（RANSAC具有很强的抗噪声能力，只要迭代次数够多，肯定能找到最优解，如果噪声大于50%，那么实际上噪声就是主要的点而不是噪声了）

基本思想：

RANSAC 通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：

  1. 有一个模型适用于假设的局内点，即所有的未知参数都能从假设的局内点计算得出。
  2. 用 1 中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点。
  3. 如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
  4. 然后，用所有假设的局内点去重新估计模型，因为它仅仅被初始的假设局内点估计过。
  5. 最后，通过估计局内点与模型的错误率来评估模型。

这个过程被重复执行固定的次数，每次产生的模型要么因为局内点太少而被舍弃，要么因为它比现有的模型更好而被选用。

对上述步骤，进行简单总结如下：

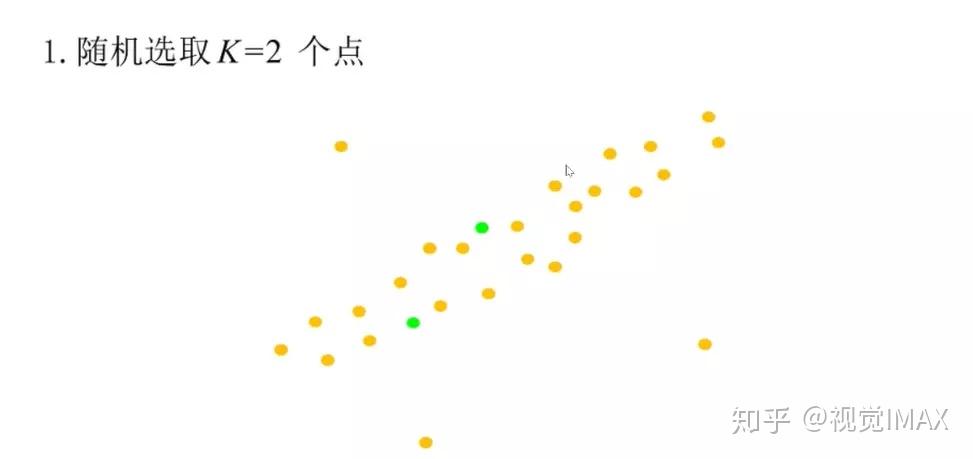
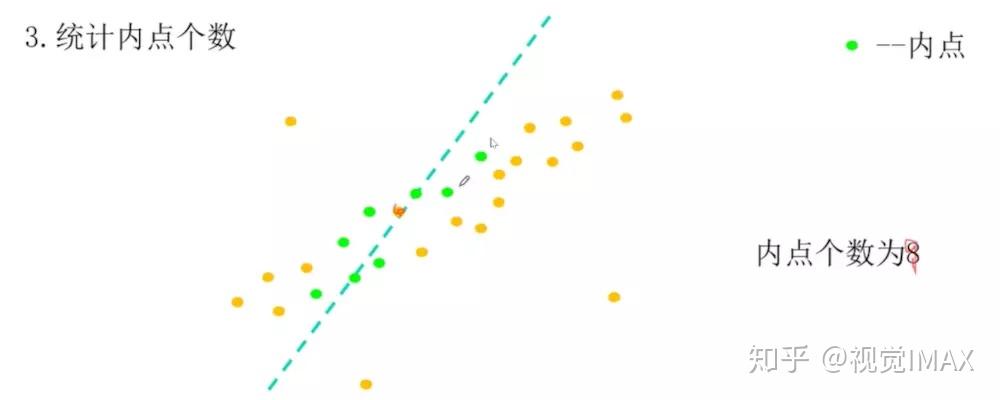
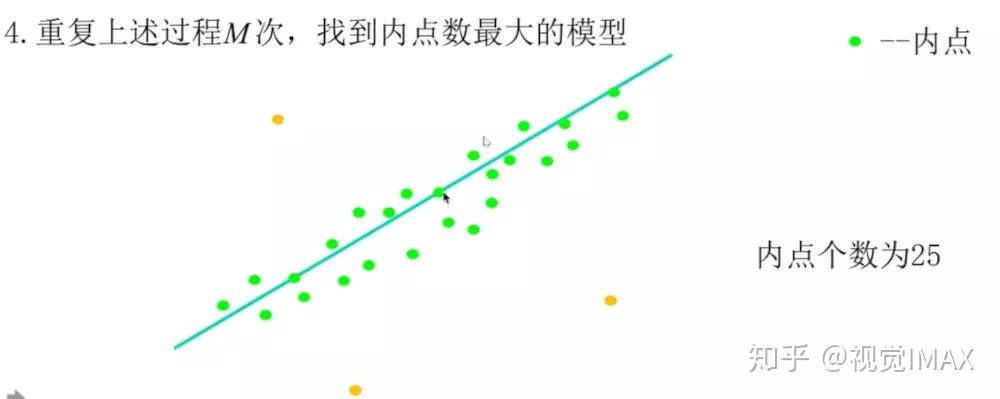
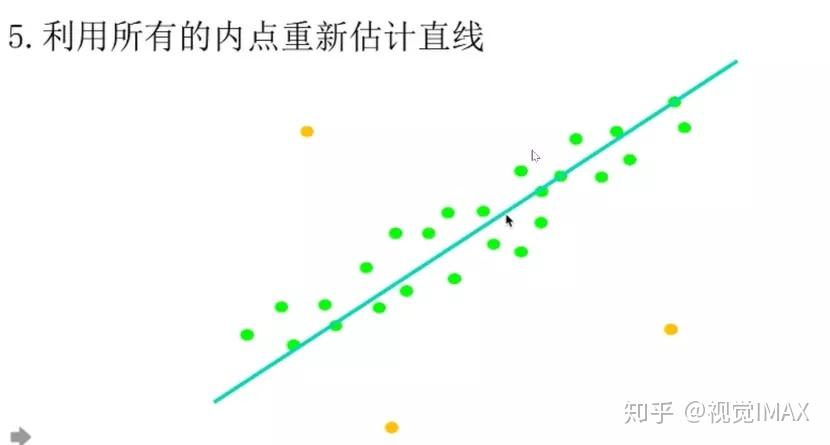
举个例子：使用 RANSAC——拟合直线

应用举例-拟合平面

  1. solvePnPRansac
  2. findFundamentalMat

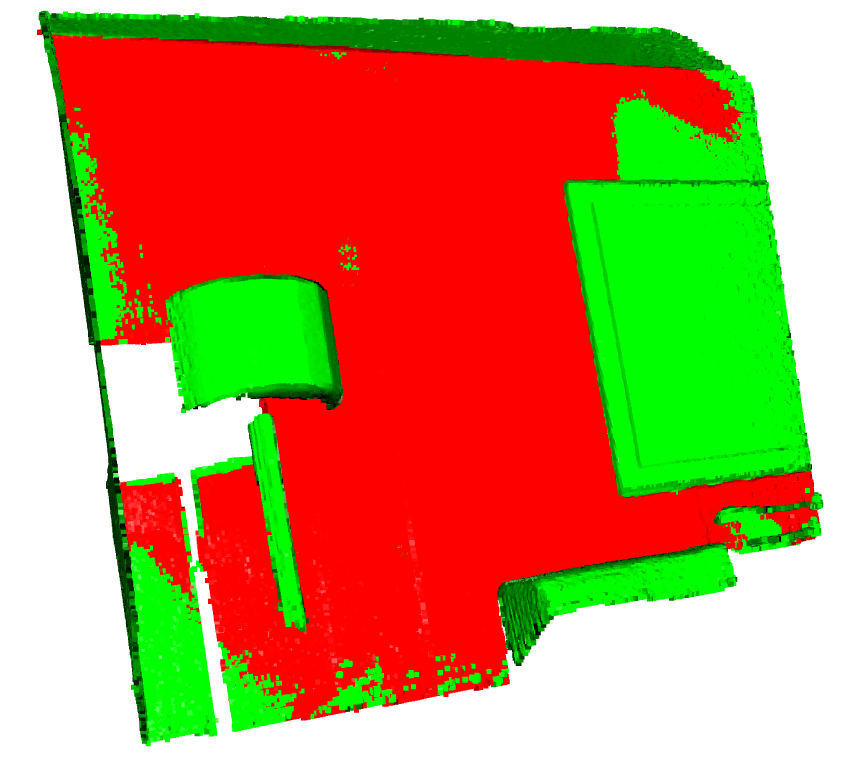
是用open3d拟合点云内的平面。

import open3d as o3d
import numpy as np
from matplotlib import pyplot as plt

'''
RANSAC算法 随机一致性采样
'''

pcd = o3d.io.read_point_cloud("./test_data/fragment.pcd")
print(pcd)
# 0.01m以内都算内点，3点确定一个平面，迭代次数为1000次
plane_model, inliers = pcd.segment_plane(distance_threshold=0.01,
                                         ransac_n=3,
                                         num_iterations=1000)
[a, b, c, d] = plane_model
print(f"Plane equation: {a:.2f}x + {b:.2f}y + {c:.2f}z + {d:.2f} = 0")

inlier_cloud = pcd.select_by_index(inliers)
inlier_cloud.paint_uniform_color([1.0, 0, 0])
outlier_cloud = pcd.select_by_index(inliers, invert=True)
o3d.visualization.draw_geometries([inlier_cloud, outlier_cloud],
                                  zoom=0.8,
                                  front=[-0.4999, -0.1659, -0.8499],
                                  lookat=[2.1813, 2.0619, 2.0999],
                                  up=[0.1204, -0.9852, 0.1215])

效果：红色为平面，绿色为噪声。

image-20210901191509153