svd
EVD-特征值分解
在理解奇异值分解之前,需要先回顾一下特征值分解,如果矩阵$A$是一个$m\times m$的实对称矩阵(即$A = A^T$),那么它可以被分解成如下的形式
$$ A = Q\Sigma Q^T= Q\left[ \begin{matrix} \lambda_1 & \cdots & \cdots & \cdots\ \cdots & \lambda_2 & \cdots & \cdots\ \cdots & \cdots & \ddots & \cdots\ \cdots & \cdots & \cdots & \lambda_m\ \end{matrix} \right]Q^T $$ 其中$Q$为标准正交阵,即有$QQ^T = I$,$\Sigma$为对角矩阵,且上面的矩阵的维度均为$m\times m$。$\lambda_i$称为特征值,$q_i$是$Q$(特征矩阵)中的列向量,称为特征向量。
注意到要进行特征分解,矩阵A必须为方阵。那么如果A不是方阵,即行和列不相同时,我们需要使用SVD。
SVD-奇异值分解
定义
奇异值分解是一个能适用于任意的矩阵的一种分解的方法: $$ M=U \Sigma V^{T} $$ 假设M是一个M *N的矩阵,那么得到的U是一个M *M的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个M * N的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V的转置是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量)。
那么我们如何求出 SVD 分解后的 $U, \Sigma, V$这三个矩阵呢?
如果我们将 A 的转置和 A 做矩阵乘法,那么会得到 $n \times n$的一个方阵 $A^TA$。既然 $A^TA$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式: $$ (A^TA)v_i = \lambda_i v_i $$ 这样我们就可以得到矩阵 $A^TA$的 n 个特征值和对应的 n 个特征向量 $v$了。将 $A^TA$的所有特征向量张成一个 $n \times n$的矩阵 V,就是我们 SVD 公式里面的 V 矩阵了。一般我们将 V 中的每个特征向量叫做 A 的右奇异向量。
如果我们将 A 和 A 的转置做矩阵乘法,那么会得到 $m \times m$的一个方阵 $AA^T$。既然 $AA^T$是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式: $$ (AA^T)u_i = \lambda_i u_i $$ 这样我们就可以得到矩阵 $AA^T$的 m 个特征值和对应的 m 个特征向量 $u$了。将 $AA^T$的所有特征向量张成一个 $m \times m$的矩阵 U,就是我们 SVD 公式里面的 U 矩阵了。一般我们将 U 中的每个特征向量叫做 A 的左奇异向量。
U 和 V 我们都求出来了,现在就剩下奇异值矩阵$\Sigma$没有求出了。由于$\Sigma$除了对角线上是奇异值其他位置都是 0,那我们只需要求出每个奇异值$\sigma$就可以了。
我们注意到:
$$ A=U\Sigma V^T \Rightarrow AV=U\Sigma V^TV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = Av_i / u_i $$ 这样我们可以求出我们的每个奇异值,进而求出奇异值矩阵$\Sigma$。
上面还有一个问题没有讲,就是我们说 $A^TA$的特征向量组成的就是我们 SVD 中的 V 矩阵,而 $AA^T$的特征向量组成的就是我们 SVD 中的 U 矩阵,这有什么根据吗?这个其实很容易证明,我们以 V 矩阵的证明为例。
$$A=U\Sigma V^T \Rightarrow A^T=V\Sigma^T U^T \Rightarrow A^TA = V\Sigma^T U^TU\Sigma V^T = V\Sigma^2V^T$$
上式证明使用了:$U^TU=I, \Sigma^T\Sigma=\Sigma^2。$可以看出 $A^TA$的特征向量组成的的确就是我们 SVD 中的 V 矩阵。类似的方法可以得到 $AA^T$的特征向量组成的就是我们 SVD 中的 U 矩阵。
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足如下关系:
$$ \sigma_i = \sqrt{\lambda_i} $$ 这样也就是说,我们可以不用 $\sigma_i = Av_i / u_i$来计算奇异值,也可以通过求出 $A^TA$的特征值取平方根来求奇异值。
奇异值分解的几何意义:
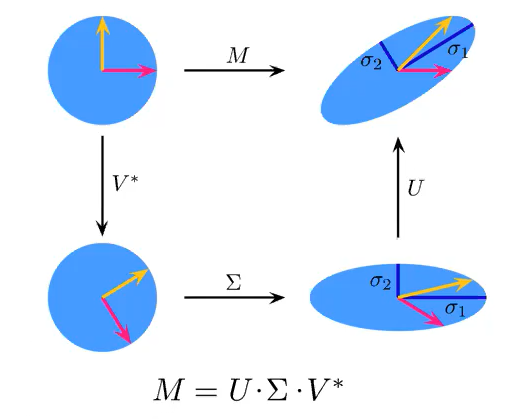
几个参考链接:
SVD(奇异值分解)小结(包含python图片压缩)
SVD用于PCA
要用 PCA 降维,需要找到样本协方差矩阵 $X^TX$的最大的 d 个特征向量,然后用这最大的 d 个特征向量张成的矩阵来做低维投影降维。可以看出,在这个过程中需要先求出协方差矩阵 $X^TX$,当样本数多样本特征数也多的时候,这个计算量是很大的。
注意到我们的 SVD 也可以得到协方差矩阵 $X^TX$最大的 d 个特征向量张成的矩阵,但是 SVD 有个好处,有一些 SVD 的实现算法可以不求先求出协方差矩阵 $X^TX$,也能求出我们的右奇异矩阵 $V$。也就是说,我们的 PCA 算法可以不用做特征分解,而是做 SVD 来完成。这个方法在样本量很大的时候很有效。实际上,scikit-learn 的 PCA 算法的背后真正的实现就是用的 SVD,而不是我们我们认为的暴力特征分解。
另一方面,注意到 PCA 仅仅使用了我们 SVD 的右奇异矩阵,没有使用左奇异矩阵,那么左奇异矩阵有什么用呢?
假设我们的样本是 $m \times n$的矩阵 X,如果我们通过 SVD 找到了矩阵 $XX^T$最大的 d 个特征向量张成的 $m \times d$维矩阵 U,则我们如果进行如下处理:
$$X’{d \times n} = U{d \times m}^TX_{m \times n}$$
可以得到一个 $d \times n$的矩阵 X‘, 这个矩阵和我们原来的 $m \times n$维样本矩阵 X 相比,行数从 m 减到了 d,可见对行数进行了压缩。也就是说,左奇异矩阵可以用于行数的压缩。相对的,右奇异矩阵可以用于列数即特征维度的压缩,也就是我们的 PCA 降维。
点对点配准使用SVD
