点云处理基础

Reference

  1. 《深蓝学院三维点云处理课程》

  2. open3d docs

点云简介

一些三维的表达形式：

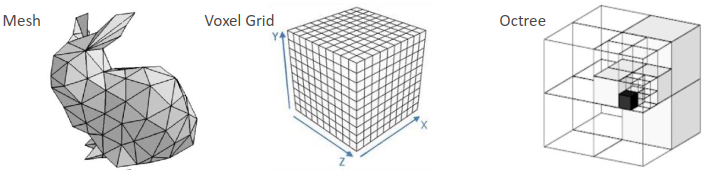
image-20220527100811864

  • mesh：多用于计算机图形学；

  • voxel grid：排列整齐、有序，可以对标二维的像素，但是空间大部分位置是空的，造成浪费；

  • 八叉树： 只向下细分内部有东西的格子，空间紧凑了，但是结构复杂，可能的计算开销相对变大。

点云：一种简单且紧凑的数据格式。

点云处理的困难：

image-20220527102324743

其中，无序和旋转不变性是深度学习方法需要想办法处理的，因为变换顺序或者旋转后输入网络的矩阵的数值就完全变了，但点云还是点云。

POINT NET就是在矩阵中的数据维度上做max pool，不管顺序怎么变，max pool的值都是相同的，解决了无序的问题。

旋转不变性依然是一个比较大的问题。

数学工具与基础算法

pca-主成分分析

b站链接：https://www.bilibili.com/video/BV1E5411E71z?from=search&seid=12219938521484233618

PCA主要用于数据降维与表面法向量估计等。

数据降维的目的用更少的空间保留尽可能多的信息。主成分就是所有数据投影到这个方向时，能够保留最大的信息（即方差最大）。假想下图中的二维点如果投影到某个方向时变成了一个点，那么就没有保留到原始的分布信息，所以要求方差最大，就是想把差异最大化，从而保留原始数据的分布特点。

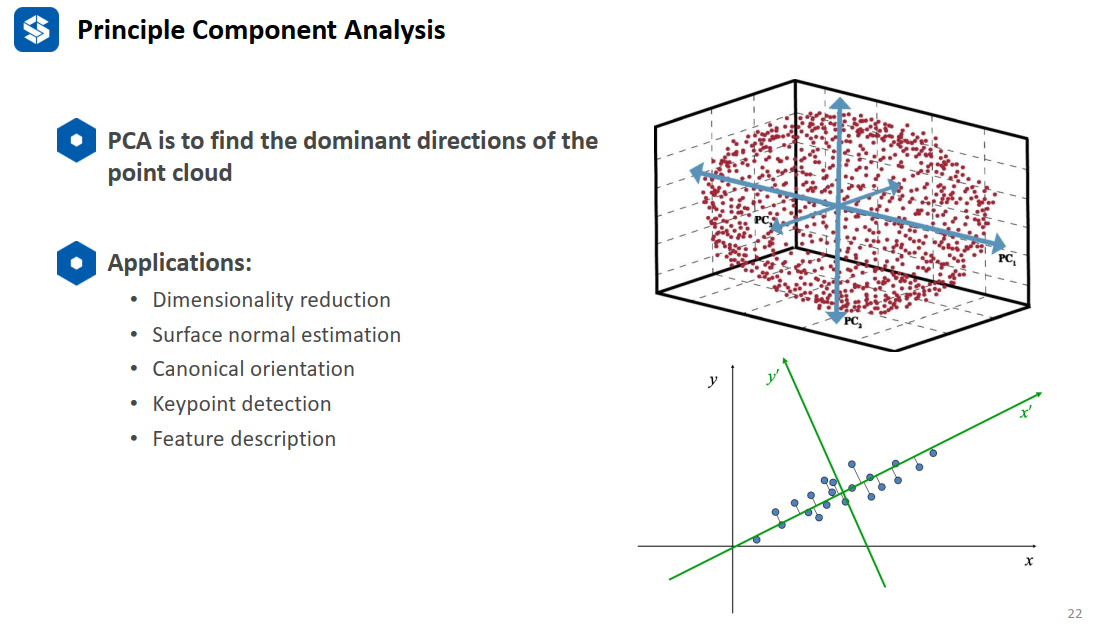
image-20210721161606188

求解主成分

协方差矩阵的推到，过程不用记：

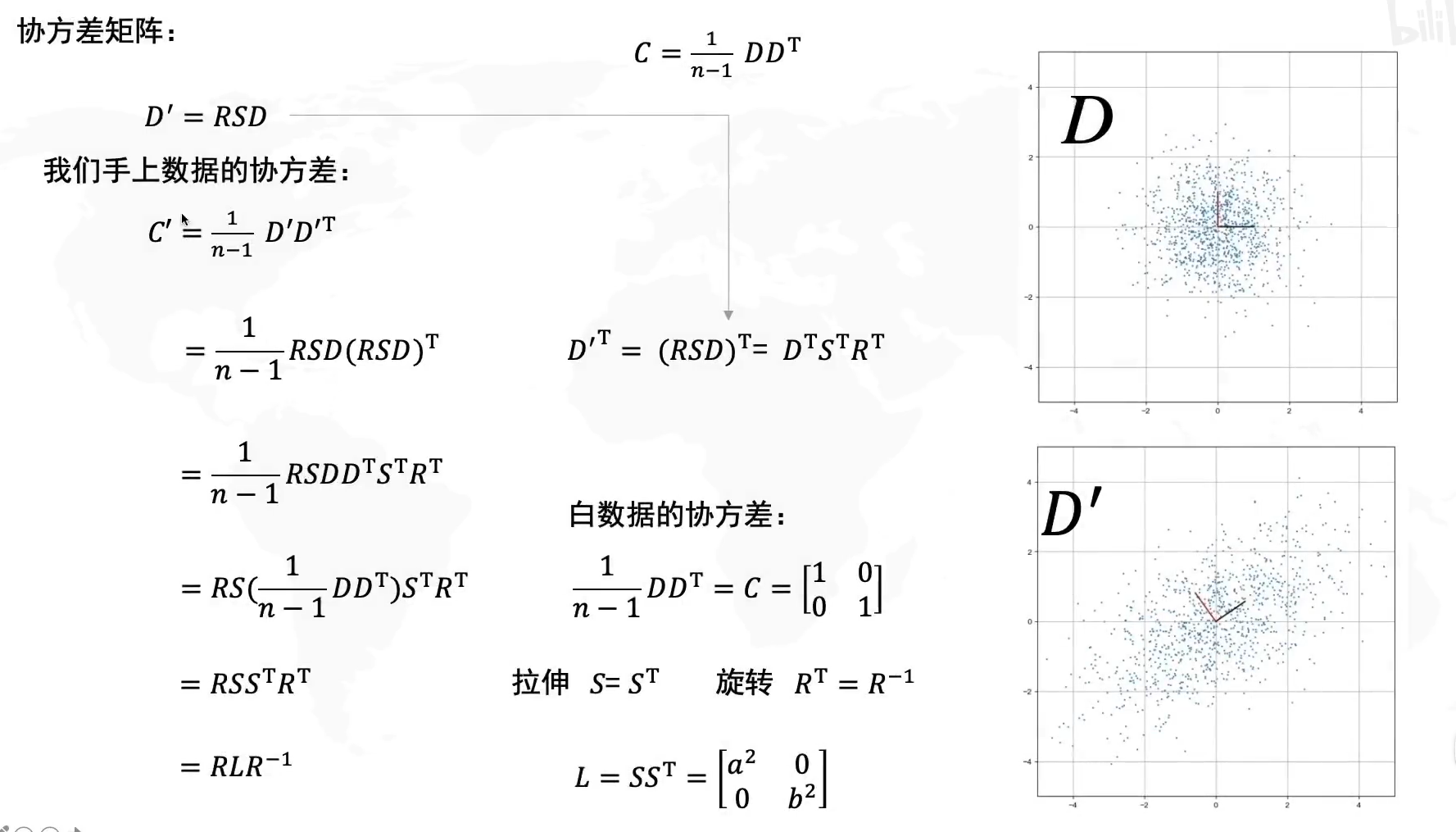
image-20210723144841574

主成分为旋转矩阵R的列向量。

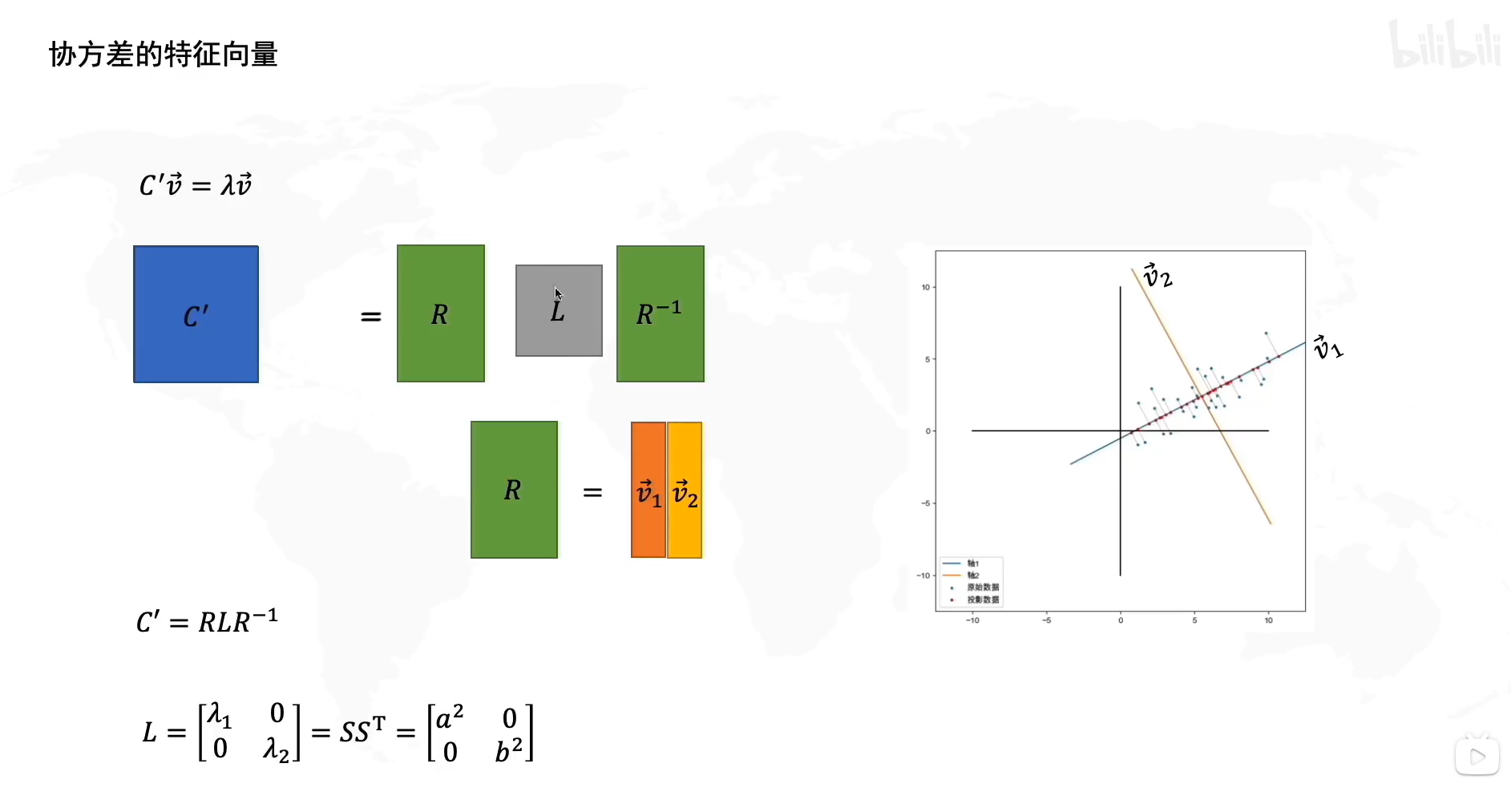
image-20210723143942632

协方差的特征值：

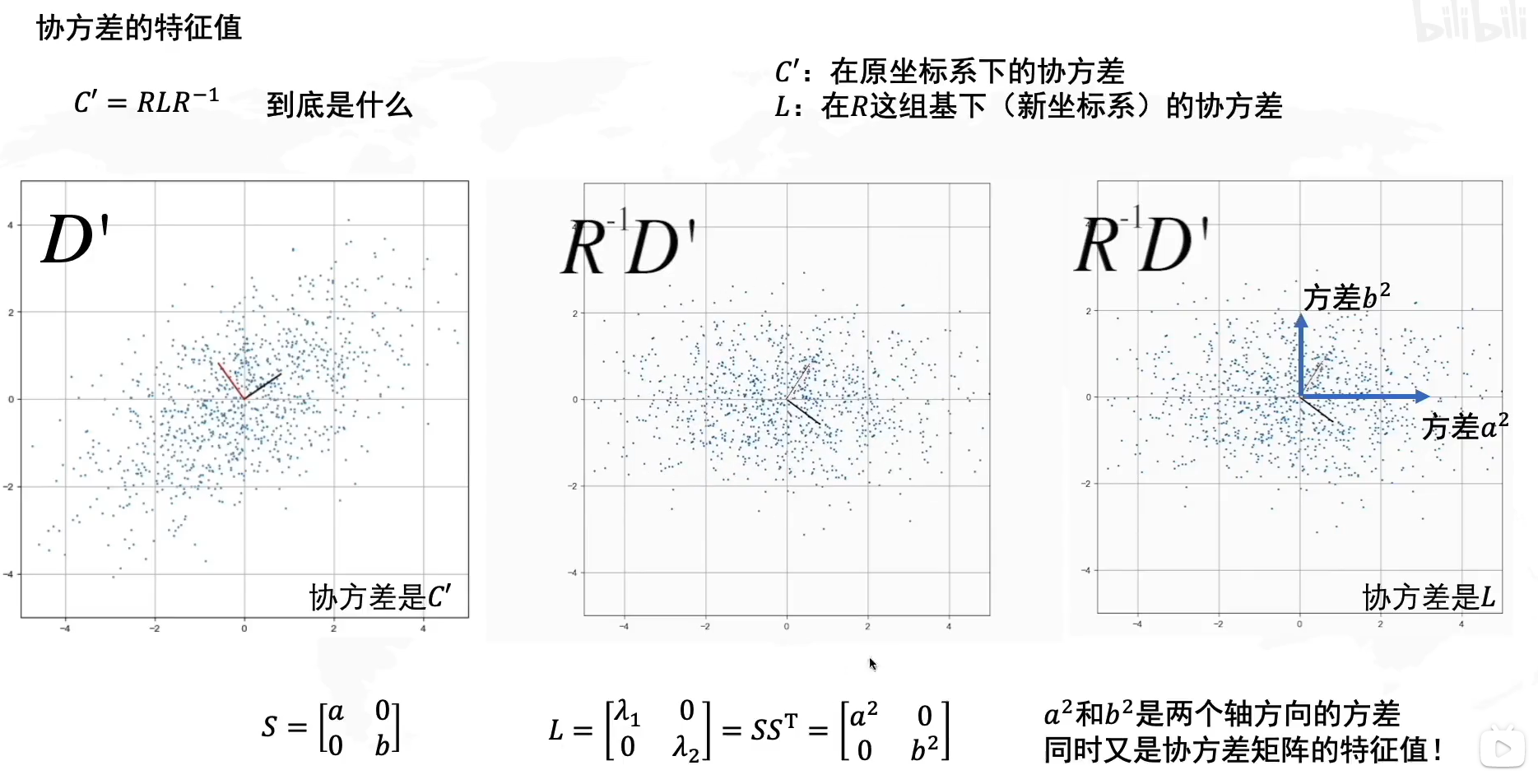
image-20210723145627502

评论区

这是挖掘数据线性分布规律的最重要算法。其实不仅仅用来降维，凡是涉及到分析数据分布特点的都可以用到。如：现在获得了某曲面大量的采样点云，要估计曲面在某采样点的法向量方向。则通过PCA分析该点及周围采样点的分布规律，找到数据点分布离散程度最大的两个正交方向，则这两个方向就近似构成曲面在该点的切平面，与此两方向正交的第三个方向就是曲面在该点的近似法矢

最初知道这个算法就是在研究点云处理、逆向工程时查文献了解的。后来开始转向机器学习又遇到这个。后面学了矩阵论加强了线代基础，把这个算法自己又推导了一遍，在看此视频之前已经从理论到直观透彻理解了

滤波

降采样

随机降采样，栅格降采样。

随机降采样

优点：速度非常快。

对于一些体量极大的点云很有效。比如一些工业大型构件（车体等）扫描出来的点云有可能达到上千万、上亿的点，直接去做处理是非常慢的，可以先做随机降采样处理到几千或者是几万的一个水平。

栅格降采样

栅格内选取一个点：

求平均或加权（慢一点但精准），随机（快但可能不精准）。

步骤如下图，注意：

体素降采样后，点云是有序的，就是栅格（体素）的顺序。

三维的坐标是(h_x,h_y,h_z)，一维数组内的索引就是下图中的h。

排序的时间复杂是O(NlogN)（快排）。所以如果不做优化整体算法是O(NlogN)。

image-20220724152633460

使用哈希表优化，能使用哈希表优化的主要原因是，我们知道最终这些点都会被放到h个容器中，每个点的ind正好代表了容器的编号，所以先把每个点放到对应的容器中，然后保留非空容器，最后在每一个容器内选择一个点。所以是使用空间节省时间。

最远点采样

先随机选一个点，然后遍历点云，选择一个最远点加入已选择点集S；

遍历点云，选择与S中所有点距离和最远的点加入S。重复这个过程。

由此优势：有些地方密度太大也只会选少部分点，得到的结果比较均衡，原始点云的分布特征也保留了下来。

但是复杂度比较高，至少是大于O(KN)的，应该是O(KlogKN)？（猜的，K是降采样后点数）

image-20220724161621153

NSS法向量空间采样

思路就是对法向量建立区间（类似直方图），比如0-360分成36个区间，每个区间内采样固定数量的点。这样最终得到的点的法向量分布比较均衡，法向量可以理解为一种几何结构特征的描述，由此NSS后由于法向量分布比较均衡，所以原始点云的几何结构特征也得到了较好保留（不会直接把一些凸起直接滤掉什么的）。

image-20220724162809013

上采样

双边滤波

先粘贴一点关于双边滤波在图像内做平滑的解释。

两个高斯权重相乘： $$ W S=e^{\left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{s}^{2}}\right)} $$

$$ w r=e^{\left(-\frac{|f(i, j)-f(k, l)|^{2}}{2 \sigma_{r}^{2}}\right)} $$

上面是二维的高斯分布，跟位置有关系，下面这个是图像的亮度差值的一维高斯分布。

img

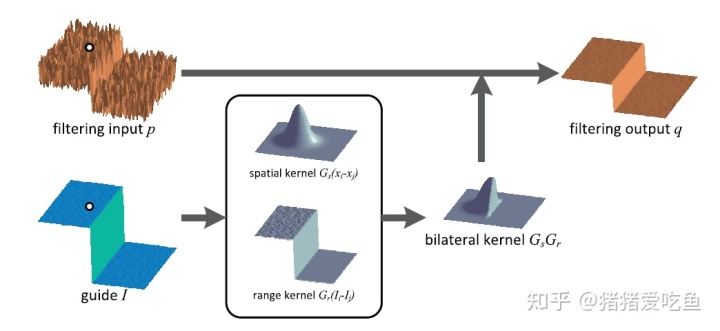
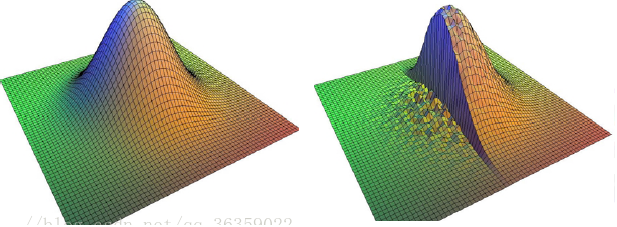
image-20220707145424837

由于在空域，像素是整齐排列的，所以在函数上采样的ws（权重）是上图左侧均匀变化的，但是在color space亮度是没有规律的，所以就是越亮度或色彩越相似，权重越高；如果在边缘区域出现剧烈的亮度变化，那么不相似的一侧分配到的权重就会很小，于是出现上图所示的“断崖式”缩减。

opencv给出的实现中，给出的双边滤波器bilateralFilter的3个主要参数如下：

bilateralFilter(src, opt, d, sigmaColor, sigmaSpace);
/*
d				邻域半径
sigmaColor		color空间的sigma值，也就是高斯分布的标准差值，值越大也就是亮度差值大的也会获得较高权重；接近无穷大时，那么退化成普通高斯滤波。
sigmaSpace		普通的空域高斯函数的标准差值。
*/

双边滤波做深度图点云补全

如下做传感器数据融合时，把稀疏的激光点云数据与图像融合，导致很多图像像素的位置没有深度信息，由此常规思路是高斯滤波用邻域深度数据得到当前像素的深度信息。

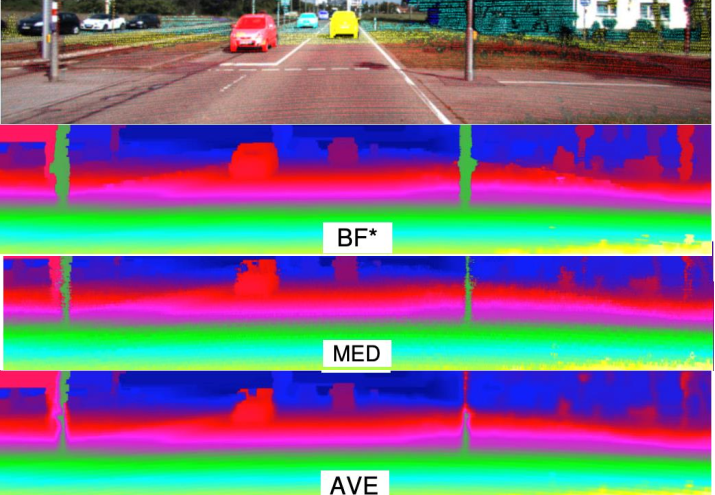
双边滤波的优化就是加入色彩信息的高斯函数，颜色相近，权值大，颜色不向近，权值小。（下图：双边，中值，均值）

image-20220724171453439

离群点去除

半径滤波

半径离群点去除，规定半径内的最少邻居数量

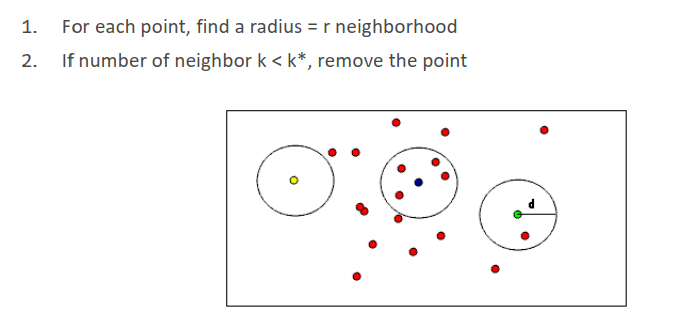
image-20220723221725983

统计滤波

m个点，计算每个点邻域内k个点的距离，把所有距离当成是高斯分布计算其均值和标准差，然后通过控制sigma前的权重只保留邻域距离的均值在指定范围的点。

所以这个方法基本上可以不用调参（比如半径）就能取得比较好的结果。所以是根据整个分布的统计信息来进行滤波的。

image-20220723222523044

open3d的接口，两个参数，基本可以不调。

print("Statistical oulier removal")
cl, ind = voxel_down_pcd.remove_statistical_outlier(nb_neighbors=20,
                                                    std_ratio=2.0)
display_inlier_outlier(voxel_down_pcd, ind)

近邻点查找

可用于法向量估计、离群点去除。knn-k近邻;radius nn-半径近邻

近邻点查找的核心思路，使用空间节约时间。由于raw点云数据是无序的，查找一个点的时间复杂度是o(n)，n个点是o(n^2)。使用一些数据结构比如KD树或者八叉树存放数据使得点云数据变得有序。

knn查找一个点的的一个近邻点(1nn)的时间复杂度是o(logn)

KD树

k-dimentional tree

每个维度都执行一次二分，本质上还是一种二叉树。如下图，按照x、y的顺序分割，除非在某一方向上不用再分割则略过。（此时的leaf_size=1）

image-20220727185309429

结构如下：（多了一些约束的二叉树）

axis:当前区域下一步要使用哪个轴分割
value:轴的位置
left,right:左右节点（分成了两个）
point_indices:包含有哪些点
image-20220727200626574

建立knn树的复杂度？

先看时间复杂度：由于需要每次用一个超平面把数据分成两半，所以需要分log(n)次，每次把数据分成两半时，需要把当前的维度排序（比如排序所有的x），快排需要nlogn，所以总体的时间复杂度为o(n logn logn)。有没有可能使用一种求中值的方法？因为目的只是分成两半。如果求中值是o(n)，那么总体时间复杂度为o(nlogn)

image-20220727194235635

查找knn

以图中自定义红点为例先说1nn，通过不断比较跟切平面的大小关系，最终定位到一个子节点g，从而确定了一个worst distance。由于这个圆与一些切平面相交了，所以需要继续考虑，先会返回s4到达s5右侧，e在最小范围内，ok，则更新worst distance，再继续运行知道满足条件。

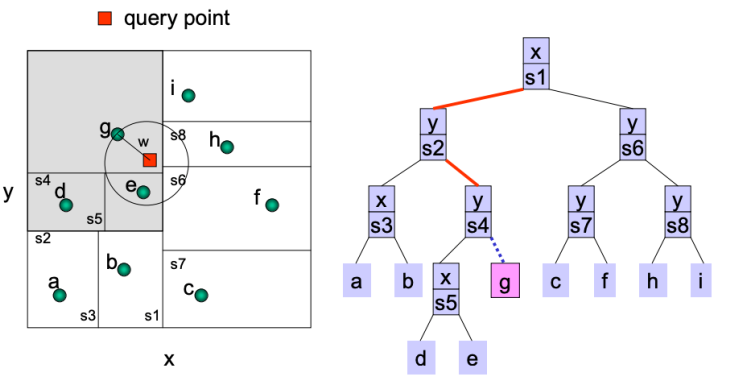
image-20220727202954678

所以，理论上1nn的查找是大于o(logn)的（到达叶子节点后可能还要继续计算），但通常可以当成是o(logn)。如果是knn的的话那么复杂度就在o(logn)到o(n)之间了。

octree

八叉树。八叉树对空间进行均匀分割，KD树是在每个维度对点的分布进行均匀分割。

对比KD树的主要优势：

  1. 可以提前结束查找，如上图KD树的图，在到达g点时，根据最坏距离画一个圆，没办法知道这个圆是否与之前的分割平面相交（栈空间，只有当前层的参数），所以只有等DFS返回各个根节点的时候才能判断是否可以终止遍历。

  2. 八叉树可以提前终止，主要原因就是因为是均匀分割，所以可以计算出树上层的各个分割平面的位置，从而判断是否可以提前终止。

image-20220802164150304

聚类