二视图三维重建与器械跟踪

参考

  1. 知乎主页：李迎松
  2. GitHub：https://github.com/ethan-li-coding
  3. 视频教程：立体视觉之立体匹配理论与实战
  4. 手术器械的光学跟踪技术研究[D]，王志刚
  5. 《视觉SLAM14讲》第7章
  6. 3D点集之间计算转移矩阵，旋转R，转移T，新增缩放s (总结全面)

关于双目立体匹配与三维重建

一种分类方式是：稠密三维重建与稀疏三维重建。

顾名思义，稀松三维重建是只讲视野内的部分点重建，稠密三维重建通常是将所有点的三维坐标都重建出来。

我们的项目是稀疏点三维重建。两种方案很多基础知识和术语是相同的

目前，学界研究的基于双目的三维重建几乎都是稠密的深度图重建，因为说实话，稀疏点重建挺简单的。稀疏点的三维重建左右点的匹配关系可以做的非常精确，所以，通常情况下，稀疏点的三维重建的精度会比稠密三维重建高很多。

稠密点三维重建

概述

从双目图像中恢复整张深度图（通常是以左摄像机坐标系为参考）。一些技术相似的任务：MVS、SFM

image-20220404225227485

场景：无人机、智能驾驶、机器人。

方法：传统算法效果还不错，近几年出现大量基于深度学习的方法（以lidar值为groundtruth）。

恢复相机运动

对于MVS或者SFM等任务，没有相机间的坐标转换关系。对极约束简洁地给出了两个匹配点的空间位置关系。于是，相机位姿估计问题变为以下两步：

  1. 根据配对点的像素位置求出 E 或者 F。（E用8点法）
  2. 根据 E 或者 F 求出 R、 t。（SVD，四组解，使用深度值为正的一组）

由于 E 和 F 只相差了相机内参，而内参在 SLAM 中通常是已知的，所以实践当中往往使用形式更简单的 E。

除了基本矩阵和本质矩阵，二视图几何中还存在另一种常见的矩阵：单应矩阵（ Homography）H，它描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上（比如墙、地面等），则可以通过单应性来进行运动估计。

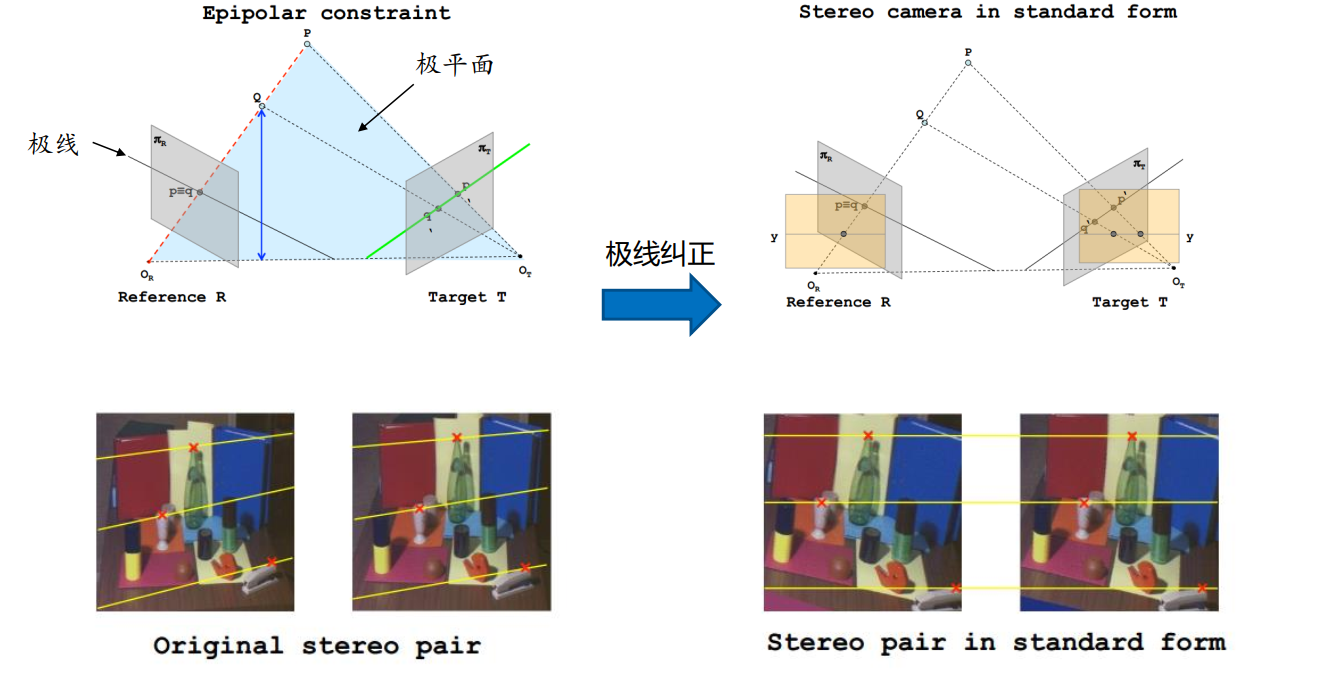
方法框架

关于极限纠正的代码，opencv也提供了相应的接口，我们自己程序内也有，但是实际操作时没用而已。

image-20220404224636480

右边是视差三维矩阵，横轴是像素坐标x,y，纵轴是视差d。C(x,y,d)记录的是左图(x,y)与右图(x+d,y)的匹配代价。

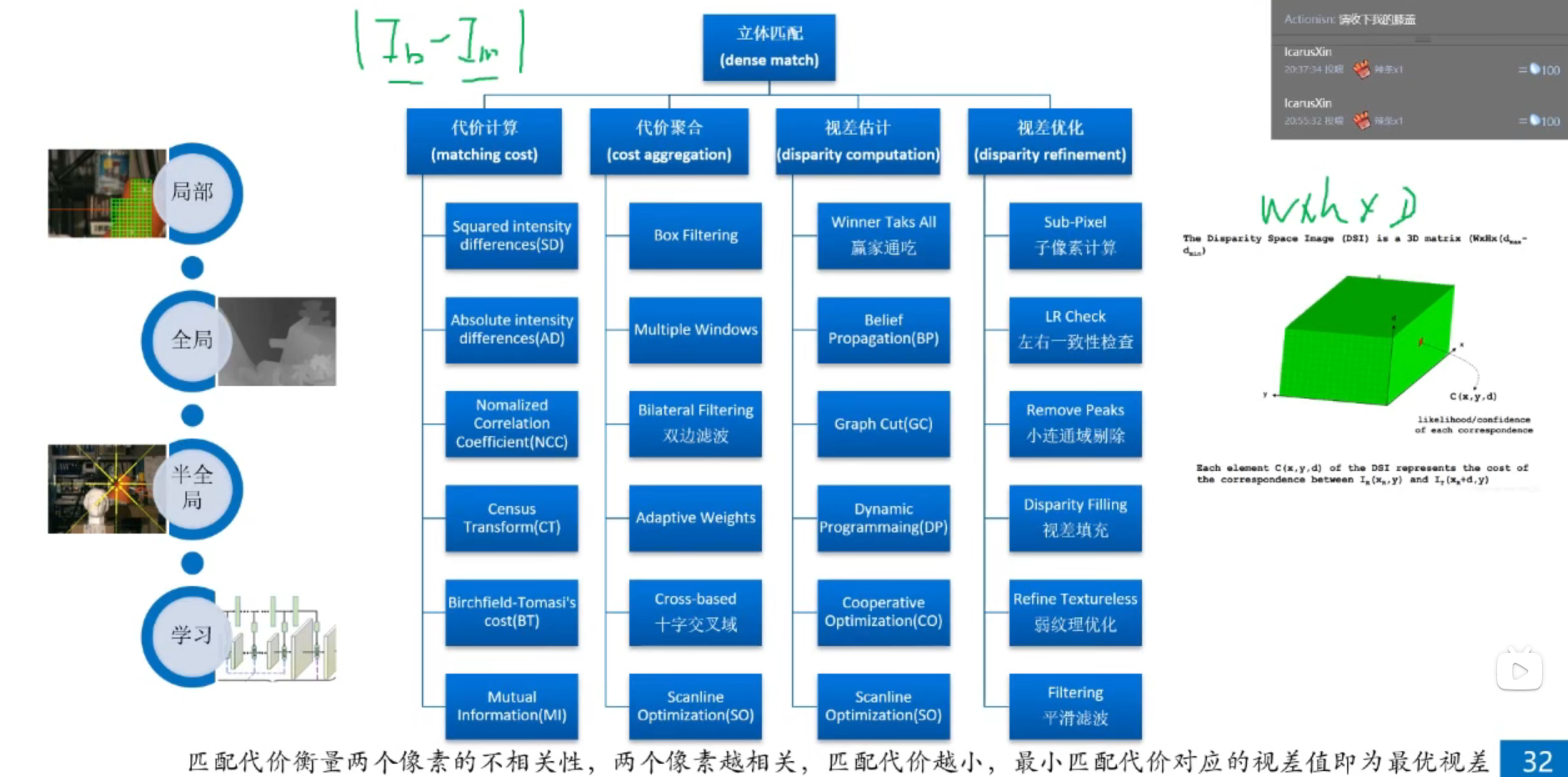
image-20220405003528506

稀疏点三维重建

场景：刚体跟踪。

image-20220405161616853

匹配与重建

已实现具有精确的双目标定信息，所以只要左右对应点正确匹配，那么就可以使用三角测量的方式将点精确重建。

三维重建的任务是计算点的三维坐标，但我们的任务还要从点信息中恢复空间变换，所以实际上是一个刚体追踪任务。需要确定哪些点是属于一个刚体的。所以这个问题不仅仅是立体匹配而已。关于点的分类，我们可以在二维图像中完成点的归类（比较困难），也可以在重建后（三维坐标）再对点进行分类。

可以看出，点的归类与立体匹配其实是完全可以分开的两个任务。立体匹配只是为了找到精准的对应关系，要在这个环节创新的话，就是找到消除误匹配的方法。距离编码使用距离信息编码同时解决了误匹配和点排序问题。如果只是为了解决误匹配，可以直接只是用距离信息，无需编码。

我个人觉得稀疏点这个任务是不太复杂的，因为我们手里的数据量其实也就只有那么几种：真实的点间距离，点的左右图像二维坐标，相机的标定参数。

距离编码代码复现

这个方法是早先2012年王志刚的硕士毕业论文出现的，后面2016年才发小论文，小论文的数据和图是直接从大论文里面拿出来的，感觉是后来挤出来的小论文。发的中科院医学4区Computer Assisted Surgery。

手术器械的光学跟踪技术研究[D]-4.4

image-20220405142439014

简述步骤：

  1. 进行编码，按照预先指定的点的顺序（比如第一个器械是前三个点…）编码角点与距离，是一一对应的（n个点）。
  2. 执行对极匹配，输出所有的匹配关系（包含错误匹配），使用三角测量将每一对匹配重建为三维坐标（长度为m*m，m>n）。
  3. 计算任意两点的欧式距离，填入矩阵形成m*m的上三角矩阵。
  4. 遍历矩阵，判断值是否与真实的器械边长相等，则在新的m*m矩阵内填入对应的距离编码。遍历结束后，对称一下矩阵，将值填满。
  5. 遍历每一行，使任意两个距离编码相加。如果等于角点编码，则匹配成功。（如果角点编码对应的是第4点，那么该点即为第4点）

随笔

三维空间点中求空间变换，其实两个点就可以，总共6个自由度，两组点就能提供6个方程。（但是会出现方向歧义，绑定手术器械后，绕中心旋转180度，靶点位置没有变化，手术器械变了）？对吗，在思考一下。（SVD提供的对应点的集合，所以是否不存在这个问题？）（两点无法建立一个参考坐标系！无法规定x、y的方向，空间变换描述的是参考坐标系之间的变换）

为什么空间中刚体跟踪通常使用的是三个点而不是两个点呢？因为两点只能绑定一条直线，无法描述一个平面，实际的刚体位置可以在绕该直线旋转的任意位置。

所以两点之间的转换是能求的，但是两点不能绑定一个三维的刚体，因为两点无法创建坐标系，所以无法描述两点与刚体的固定转换。

关于SVD，因为SVD的输入是对应点的集合，所以计算是没问题的。但是如何确定对应点关系呢？如果是2个点，从检测手段来看，你根本不知道哪个是点1哪个是点2。另外，不能是等腰三角形，这样绕中轴旋转180度靶点没有变。

使用大小不一的靶点？