射影变换与二视图几何

参考

  1. 《计算机视觉中的多视图几何》 第二版 （太数学了）
  2. 基于局部特征的图像与点云配准研究[D]
  3. 《视觉SLAM 14讲》
  4. 知乎：射影平面的直观理解
  5. 维基百科：单应性
  6. opencv: Feature Matching + Homography to find Objects
  7. 二视图从运动到结构—-对极几何和基础矩阵

射影空间与射影变换

射影空间

齐次坐标

image-20220321114417446

点、直线的齐次表示

image-20220321115621439

射影空间

n维射影空间用n+1维（除去全0）齐次向量组成。

知乎：射影平面的直观理解

射影空间只是一组齐次向量的集合，它是为了方便运算而被制造出来，其实没有必要去研究他的物理或几何意义，重要的是关注射影变换

射影变换

射影空间是最一般的空间变换。

多视图几何几何给出的比较专业的定义如下，分为几何定义与代数定义。

维基百科：单应性在计算机视觉领域中，空间中同一平面的任意两幅图像通过单应性关联在一起（假定是针孔相机）。比如,一个物体可以通过旋转相机镜头获取两张不同的照片(这两张照片的内容不一定要完全对应,部分对应即可),我们可以把单应性设为一个二维矩阵M,那么照片1乘以M就是照片2。

基于局部特征的图像与点云配准研究[D]中，关于2D射影变换的描述：（其内容几乎来自多视图几何一书）

image-20220321150106448

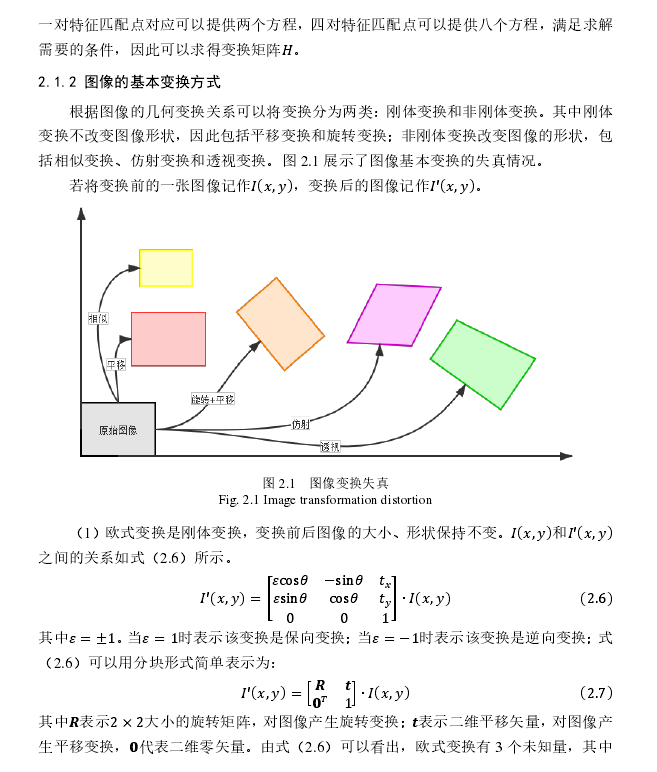
image-20220321150136237

image-20220321150512847

关于透视变换（perspective）与射影变换（projective）的区别：很多地方并不区分透视变换与射影变换。

透视变换是射影变换的一种特殊场景。（参考书P25）

image-20220321155655449

区别：如图，两个透视变换的复合一般不是透视变换，而是射影变换。

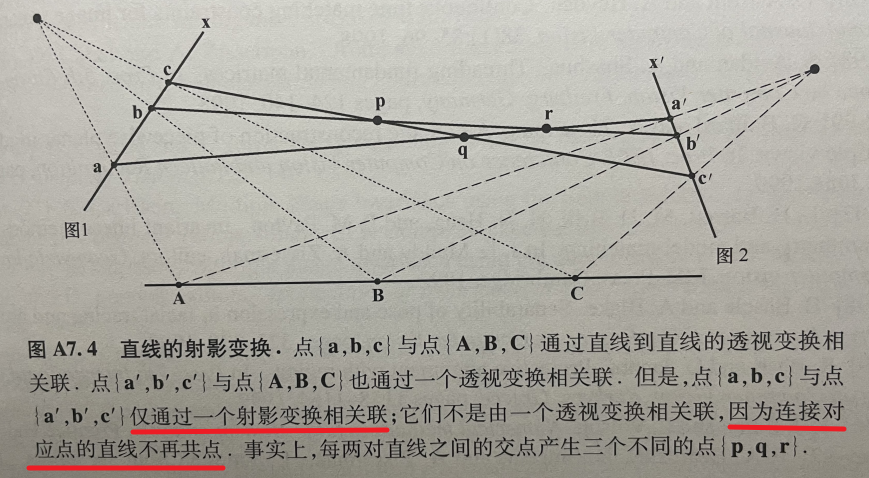
image-20220321160030395

比如opencv的getPerspectiveTransform方法，字面意思就是改变给定图像的透视图。（是在改变给定的一张图，射影变换通常是在两张图之间寻求变换（相当于更换相机位置重新拍了一张图），比如opencv: Feature Matching + Homography to find Objects）

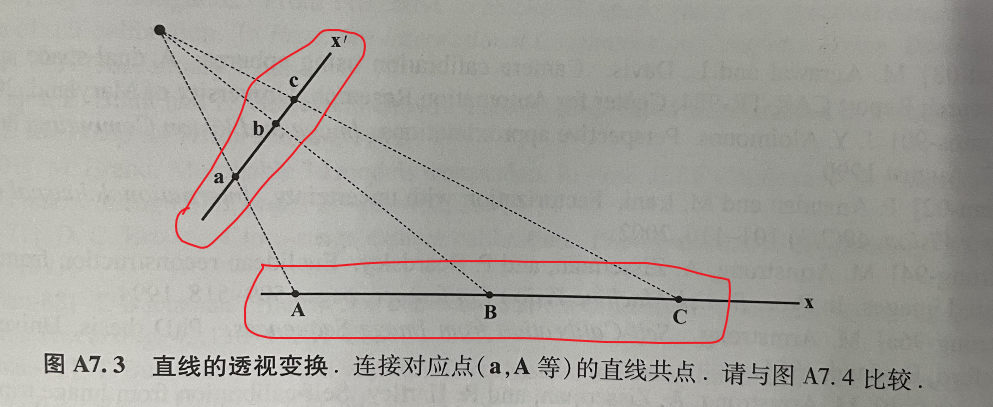
image-20220323202307667

# In Perspective Transformation, we can change the perspective of a given image or video for getting better insights into the required information.
cv2.getPerspectiveTransform method 
Parameters: 
src: Coordinates of quadrangle vertices in the source image.（原图像四边形顶点，像素坐标）
dst: Coordinates of the corresponding quadrangle vertices in the destination image.（期望的目标图像四边形顶点，像素坐标）

所以，应该从上下文理解意思，不要太纠结字眼。透视一词来自的中心投影，比如相机成像、针孔模型、人眼。（通常）

快速分辨透视变换与射影变换。（图3是图像拼接）

image-20220323204243319

《视觉SLAM14讲》中也给出类似定义：

image-20220321153212134

image-20220321153251128

求解

齐次方程有8个自由度，需要8个线性方程组，一组对应点能提供两个方程，至少需要4组对应点。

使用cv2.getPerspectiveTransform提供精准四组点对可以求得变换矩阵。

在特征匹配的场合，对应点可能出现无匹配，并且匹配对数可能远大于4对，可以使用cv2.findHomography，使用最小均方误差或者RANSAC方法优化输出结果。

摄像机模型

摄像机模型已经比较清楚了，相关的常规一点的链接比如。相机模型 16个参数

参考书内使用齐次坐标详细推导了摄像机模型P的形成。参考书 #6.1

image-20220322111246449

需要注意的是，P是将3D投影到2D，是3X4矩阵，所以P是作用到世界坐标上的，x=PX。所以，R和t也是从世界坐标系到相机坐标系的转换（相机坐标系是中间过程）。 $$ \widetilde{\mathbf{X}}_{\mathrm{cam}}=\mathrm{R}(\widetilde{\mathbf{X}}-\widetilde{\mathbf{C}}) $$ 其中，C~代表摄像机中心在世界坐标系中的坐标。

求解

通过相机标定流程获取相机矩阵。

求解外参可以使用PnP方法。[^PnP（ Perspective-n-Point）]是求解 3D 到 2D 点对运动的方法。它描述了当知道 n 个 3D 空间点及其投影位置时，如何估计相机的位姿。如果两张图像中其中一张特征点的 3D 位置已知，那么最少只需 3 个点对（需要至少一个额外点验证结果）就可以估计相机运动。

opencv提供了solvePnP函数来解决此问题。点对比较多的时候可以使用solvePnPRansac()消除噪声，提高鲁棒性。

相机标定（3） opencv中solvePnPRansac()和solvePnP()计算外参数

二视图几何

基本矩阵

基本矩阵是对极几何的代数表示。

它表示在第一幅图像上的一个点到另一幅图像上与之对应的对极线的映射。是点到直线的映射。

img

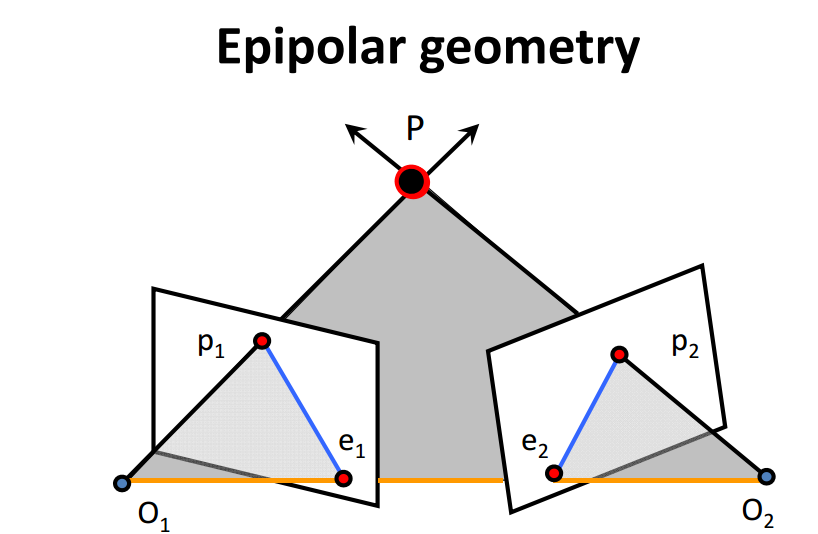
性质

image-20220321171505518

image-20220321172244630

求解

书上有介绍使用8点法或者7点法等数学方法求解F，但那是在未知相机参数的情况下。在双目相机的应用中，相机标定后，可以很轻松的使用上面红线的公式求出基本矩阵F。

本质矩阵

博客讲得比较清楚。二视图从运动到结构—-对极几何和基础矩阵

博客是从本质矩阵E讲到基本矩阵F的，参考书是先将F再讲E，不同的切入而已。

注意，叉乘转矩阵运算的方法：

img

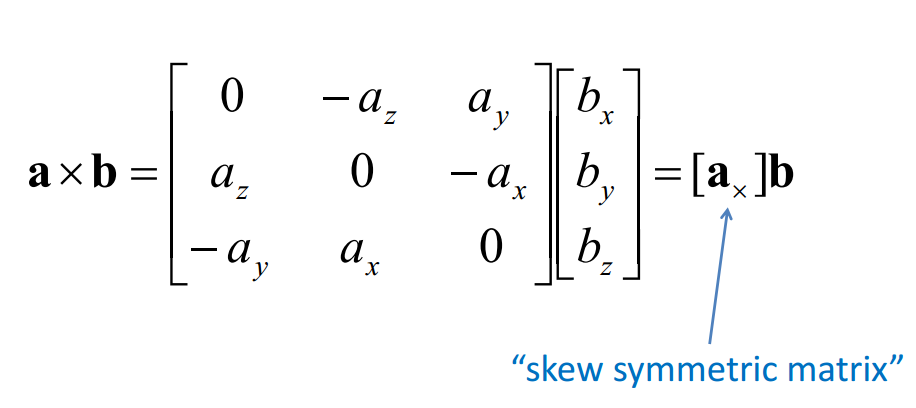
由基本矩阵恢复E： $$ \mathrm{E}=\mathrm{K}^{\prime \top} \mathrm{FK} $$ 从无标定参数的二试图求解本质矩阵：（14讲——本质矩阵）

本质矩阵只有5个自由度，照理说最少只需要5组点对即可求解，但是比较麻烦，所以通常使用8点法求解（8组）。（从工程实现角度考虑，由于平时通常会有几十对乃至上百对的匹配点，从 8 对减至 5 对意义并不明显。）