2D计算机视觉——原理、算法及应用
参考
《2D计算机视觉——原理、算法及应用》
第3章 空域增强
算数运算:
图像相减:体现两图的差别,可用于运动检测。
对比度拉伸:增加原始图像里某两个灰度值的动态范围实现对比度的拉伸。
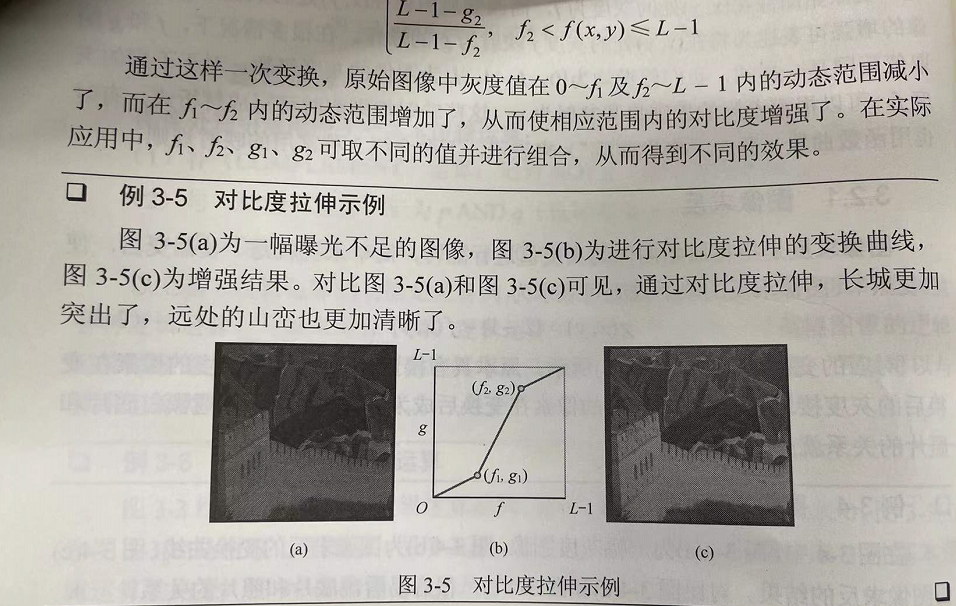
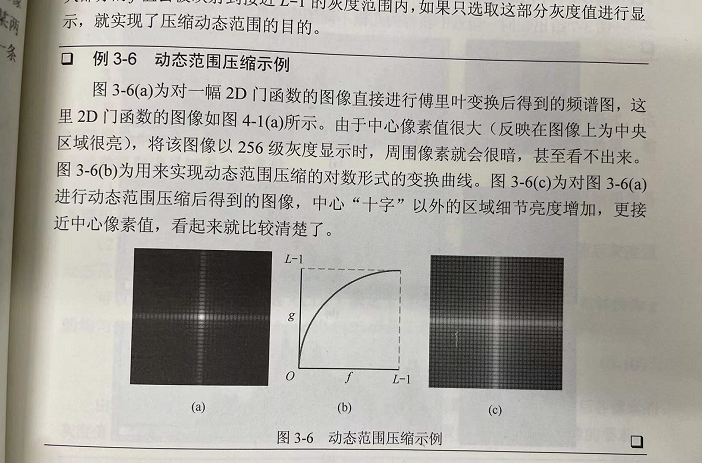
动态范围压缩:
和对比度拉伸相反目的相反,看函数图就知道了。
直方图
使用直方图统计图像的亮度分布情况。
直方图均匀化:使用累积分布函数CDF使得直方图分布均匀。
直方图规定化:把直方图变成预期的形状。
滤波
平滑(模糊)
锐化
第4章 频域增强
傅里叶变换在这个应用中的应用:把一个关于图像亮度的函数从空域(位置与亮度的关系)转化到频域(频率与亮度的关系)。
https://www.zhihu.com/question/21040374。连接中是从时域变换到频域。

第7章 图像分割
在对图像的研究和应用中,人们往往仅对图像中的某些部分感兴趣,这些部分常称为目标或前景(其他部分称为背景),一般对应图像中特定的、具有独特性质的区域。为了辨识和分析目标,需要将这些区域分离并提取出来,如进行特征提取。

先不管串、并行,分割的主要依据是检测边界或者检测区域,由此划分图像。
微分边缘检测
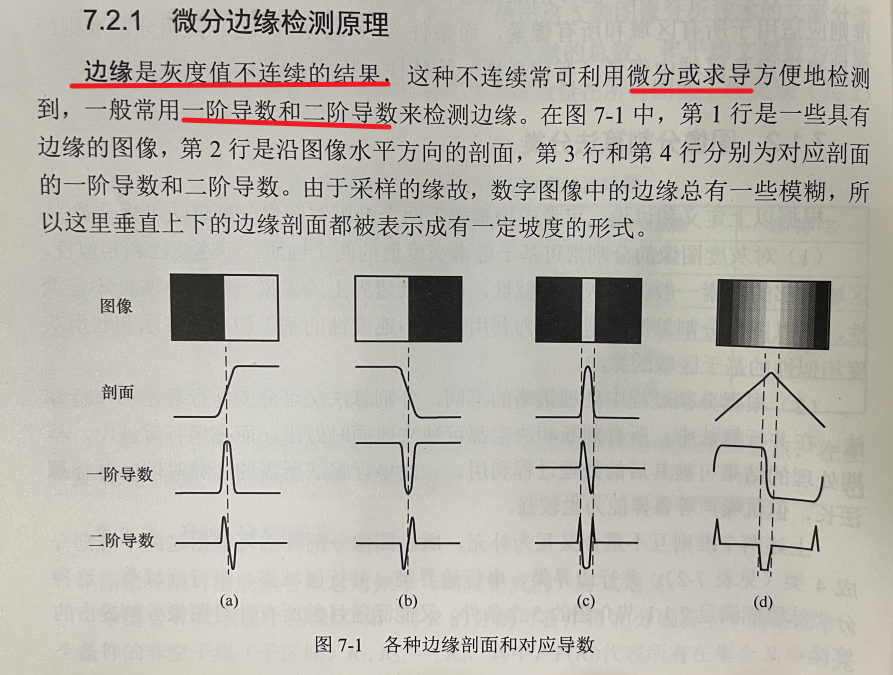
但是,图像是离散并非连续的,所以不能直接求导。所以数字图像的求导是利用差分来近似微分的。
二维的差分使用卷积来实现。
几个常用的梯度算子(一阶倒数算子/卷积模板)如下:
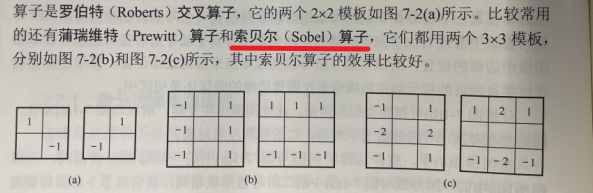
基于灰度相似性的区域检测
阈值分割
区域生长
在实际应用区域生长技术时,需要解决三个问题:
(1) 选择或确定一组能正确代表所需区域的种子像素。
(2) 确定在生长过程中能将相邻像素包括进来的生长(或相似)准则。
(3) 确定让生长过程停止的条件或规则。
第8章 基元检测
基元检测本质上还是图像分割。
角点检测
二阶导
哈里斯
使用局部模板两个方向的梯度来定义。卷积的情况下,梯度的平方和也就是领域灰度值平方差的和。

积分角点检测
使用圆形模板遍历每一个点,比较模板内其它点与中心点(核)的灰度值差异,小于阈值则记为“相同”,统计相同区域的面积比例。
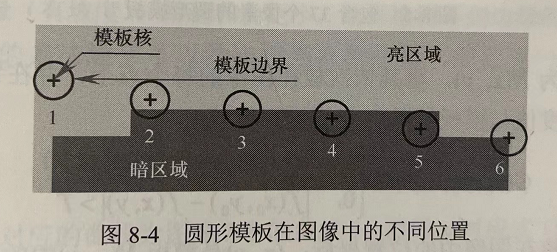
可以发现,当中心点(核)恰好在角点上时,该面积可以取最小值,其它大多数时候面积大小都是大于2分之1的。
哈夫变换
图像空间到参数空间的变换。
滤波
NR基础篇上——均值滤波、高斯滤波、双边滤波:https://zhuanlan.zhihu.com/p/422899763
OpenCV双边滤波详解及实代码实现:https://blog.csdn.net/qq_36359022/article/details/80198890
均值滤波
太简单,略过。
高斯滤波
使用高斯卷积核。
当样本数据 X 是一维数据(Univariate)时,高斯分布遵从下方概率密度函数(Probability Density Function):
其中
双边滤波
两个高斯权重相乘:
$$ W S=e^{\left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{s}^{2}}\right)} $$ $$ w r=e^{\left(-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)} $$上面是二维的高斯分布,跟位置有关系,下面这个是图像的亮度差值的一维高斯分布。
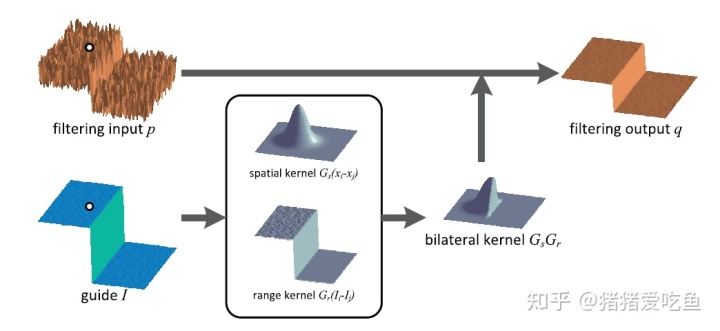
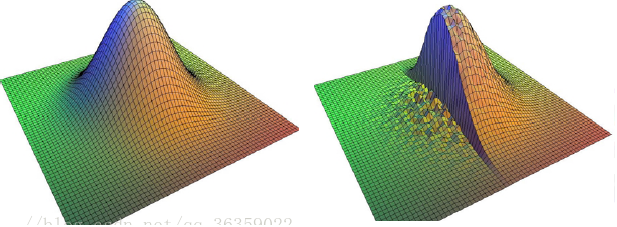
由于在空域,像素是整齐排列的,所以在函数上采样的ws(权重)是上图左侧均匀变化的,但是在color space亮度是没有规律的,所以就是越亮度或色彩越相似,权重越高;如果在边缘区域出现剧烈的亮度变化,那么不相似的一侧分配到的权重就会很小,于是出现上图所示的“断崖式”缩减。
opencv给出的实现中,给出的双边滤波器bilateralFilter的3个主要参数如下:
bilateralFilter(src, opt, d, sigmaColor, sigmaSpace);
/*
d 邻域半径
sigmaColor color空间的sigma值,也就是高斯分布的标准差值,值越大也就是亮度差值大的也会获得较高权重;接近无穷大时,那么退化成普通高斯滤波。
sigmaSpace 普通的空域高斯函数的标准差值。
*/